За първата ми публикация свързана с квантитативно инвестиране съм избрал паритет на риска.

Това е стратегия, която разпределя инвестиционното портфолио на база риск.

С други думи, вместо тежестта на всяка компания да се изразява като равна сума пари тук те интересува да имаш изравнен риск.

В края на тази статия ще научиш:

1. Как да извличаш данни за акции.
2. Как да създадеш портфолио с равно разпределен по тежест риск.
3. Как да създадеш портфолио с ограничение на неговата възвръщаемост.

Кратка история

През 90-те години на 20-ви век Bridgewater Associates бяха една от първите компании за управление на активи използваща паритет на риска. В момента имат около $200 милиарда AUM и са един от най-големите хедж фондове в света.

Каква е целта?

Основната цел трябва да бъде да получиш оптимална доходност срещу определено ниво на риск.

Проблемът с портфейлите, които разчитат на тежест за сума пари е, че не всяка компания носи еднакъв риск.

Ако „претеглиш“ две акции едната винаги носи повече риск. Съответно възвръщаемостта на портфолиото ще бъде доминирана от по-високорисковите акции. Инвеститорите използват паритет на риска, за да избегнат този проблем.

В миналото на разни професори им е отнело десетилетия да разработят и развият този анализ.

Днес ще ти покажа как можеш да я използваш с помощта няколко реда Python и малко желание да отделиш 5 минути от времето си.

За да е реално портфолиото ще включа компаниите от дивидентното ми начинание.

1. Извличане на данните за компаниите.

Първо трябва да се импортнат пакетите за извличане на данни. В този пример ще използвам yfinance и Riskfolio-Lib за паритетния анализ.

!pip install pybind11
!pip install riskfolio-lib
!pip install yfinance

import yfinance as yf
import riskfolio as rp
import warnings
warnings.filterwarnings("ignore")

След импортирането направи списък с компаниите, които искаш да анализираш.

Избрал съм период от 20г.

# Tickers we need data for.
assets = ["FRG", "BBY", "ABBV", "AVGO", "AMGN", "AQN", "GILD", "INTC", "AEP", "PG", "MPW", "EPD", "STX", "VZ", "DLX"]

# Sort tickers.
assets.sort()

# Download data
data = yf.download(assets, start="2002-11-30", end="2022-11-30")

# Compute non-compounding, daily returns.
returns = data['Adj Close'].pct_change().dropna()

2. Създаване на портфолио с равна тежест за риск.

Riskfolio-Lib ще изчисли тежестта на всяка акция и ще го разпредели поравно.

port = rp.Portfolio(returns=returns)

port.assets_stats(method_mu='hist', method_cov='hist', d=0.94)

w_rp = port.rp_optimization(
    model="Classic",  # Use historical.
    rm="MV",  # Use mean-variance optimization.
    hist=True,  # Use historical scenarios.
    rf=0,  # Set risk free rate to 0.
    b=None  # Don't use constraints.
)

1. Изгради обект с възвръщаемостта на акциите.
2. Прецени очакваната възвръщаемост и ковариацията въз основа на исторически данни.
3. Чрез оптимизация на средната дисперсия ще намериш теглото на паритета на риска.

Riskfolio-Lib улеснява визуализацията.

ax = rp.plot_pie(w=w_rp)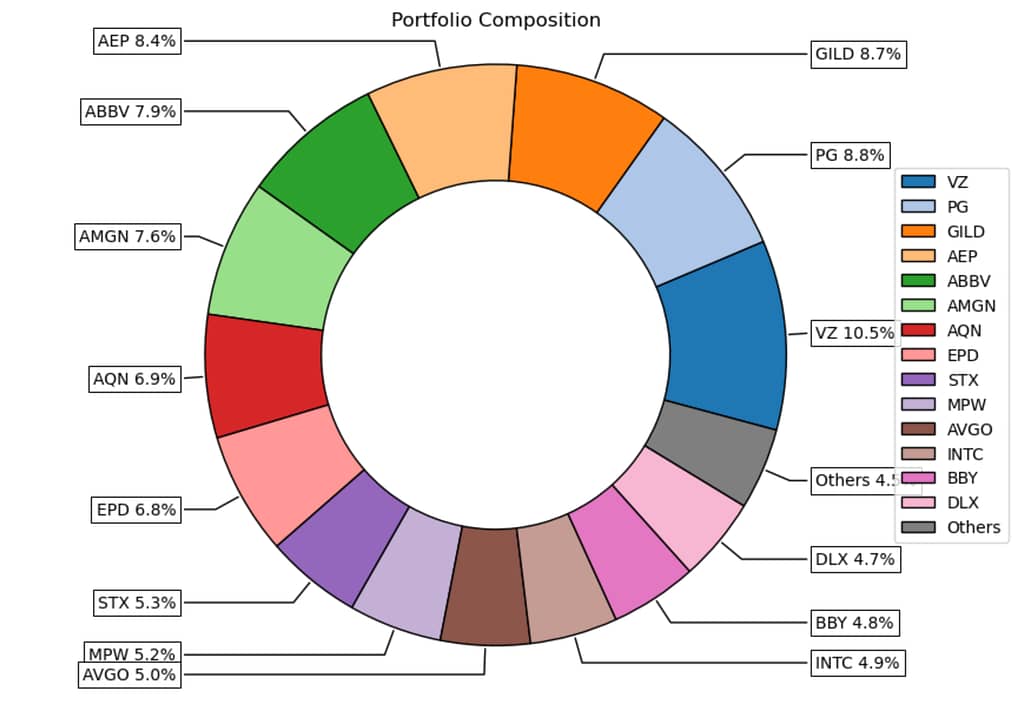

По-рисковите акции получават по-малък „дял“. Тежестта на риск на всяка компания е равна.

Ето го и самото разпределение на риск.

# Show the risk contribution for each asset is equal.
ax = rp.plot_risk_con(
    w_rp,
    cov=port.cov,
    returns=port.returns,
    rm="MV",
    rf=0,
)

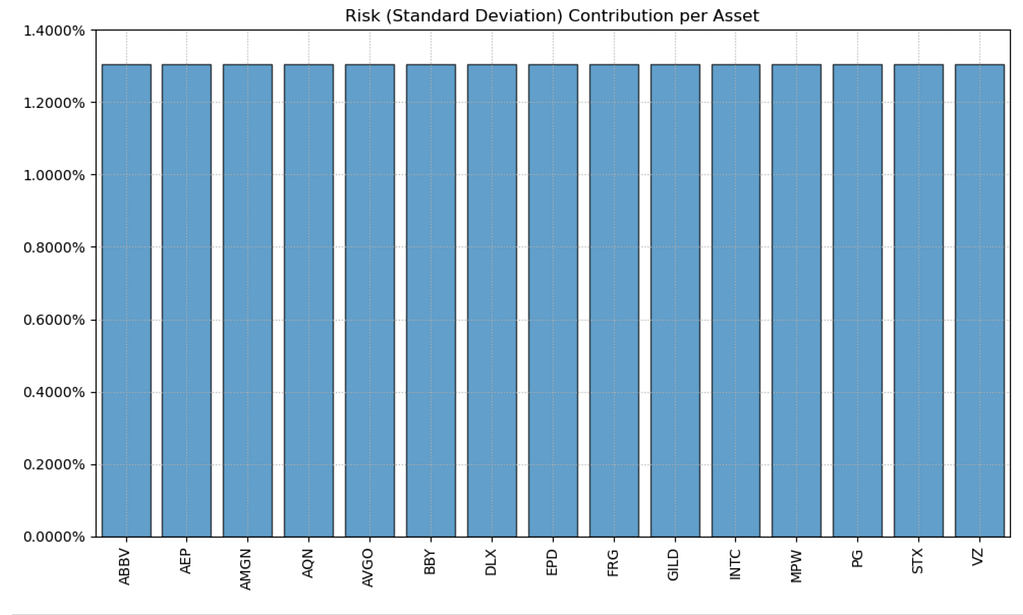
Напълно очаквано всички са равни.

3. Ограничение за минимална възвръщаемост

Една от критиките на паритета на риск е, че без ливъридж имаш по-слаба възвръщаемост.

Нека добавим тежест към по-високорисковите акции, за да увеличим възвръщаемостта на портфолиото.

port.lowerret = 0.0007

# Estimate the optimal portfolio with risk parity with the constraint
w_rp_c = port.rp_optimization(
    model="Classic",  # Use historical.
    rm="MV",  # Use mean-variance optimization.
    hist=True,  # Use historical scenarios.
    rf=0,  # Set risk free rate to 0.
    b=None  # Don't use constraints.
)

Както показах по-рано изобразяването става много лесно.

ax = rp.plot_pie(w=w_rp_c)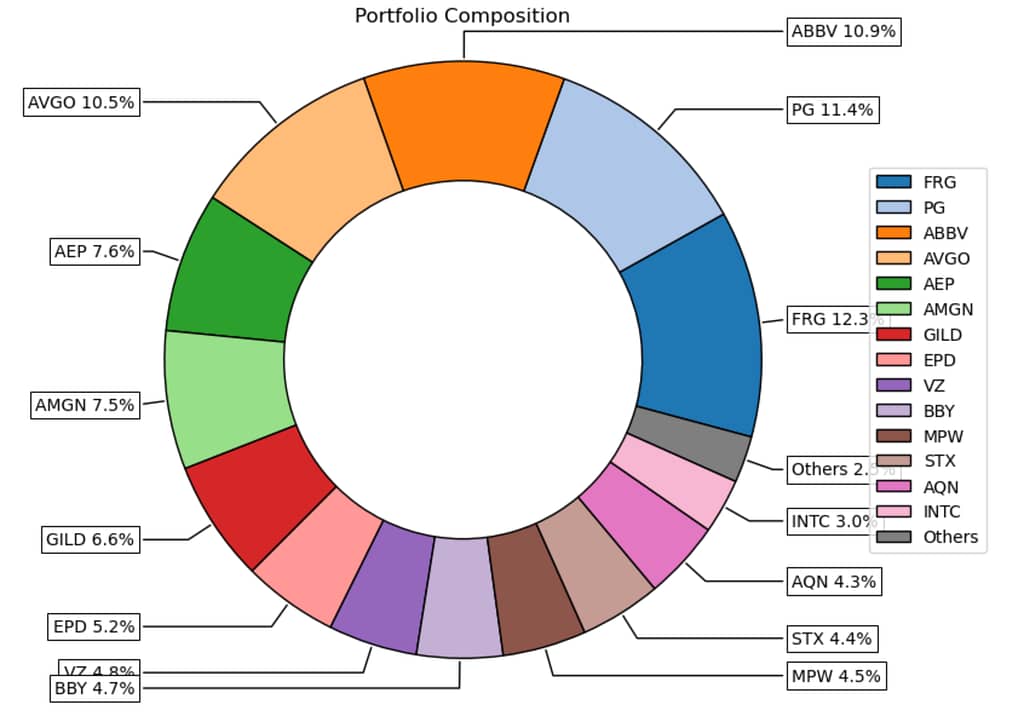

А това е приносът към риск за всяка компания.

ax = rp.plot_risk_con(
    w_rp_c,
    cov=port.cov,
    returns=port.returns,
    rm="MV",
    rf=0,
)

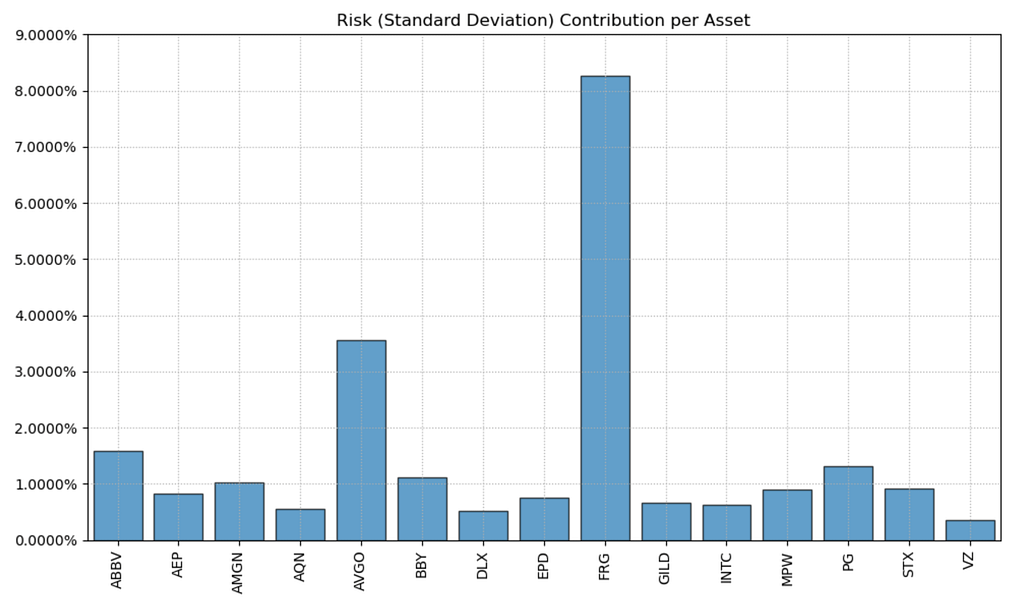
Вече не са равни. Приоритизират се по-рискови компании с повече риск, което увеличава възвръщаемостта на портфолиото.

В някоя от следващите статии ще публикувам по-подробен пример с малко повече параметри.